The Science of Refrigeration Supporting Notes
These notes provide more detailed information about the concepts explained in the videos in this section.
How do you know if your refrigerator is efficient?
How can you reduce the amount of electricity used?
How do you measure efficiency?
This article starts by looking at concepts which are so obvious that everyone thinks ”why are we talking about these simple things when there are such important issues we need to address in the world of cooling”. But sometimes it’s very useful to have an understanding of the rules and what lies behind them. This article deals only with the laws applied to refrigeration processes. This document is intended as an introduction to support the Fantastic Fridges material.
Energy
Using the laws of physics may sound intimidating but we are working with basic ‘classical’ physics that help explain the limits to what can be achieved and why.
“Energy cannot be created or destroyed” (The first law of physics) So just what is Energy? Energy is the property of a physically identifiable object (such as a gold brick) which allows it to do measurable work on another object. Energy is always conserved; it can neither be created nor destroyed. This simple fact is the First Law, one of the most important laws of physics. It is sometimes referred to as the Law of Conservation of Energy.
The total amount of energy in the Universe is constant. Energy is the currency of nature. No process or event can occur without energy being transferred. Heat is one form of energy (others include electrical, chemical and nuclear). Refrigeration is concerned with moving heat, so we will focus on that. The temperature of our gold brick can be raised by supplying it with energy. But to cool the brick, the brick itself has to supply energy to something else. It can dissipate energy in the form of microwaves such as heat or light (if it is red-hot!). But an external source cannot focus on the brick and extract energy. It's like asking why the target cannot send a bullet back to a gun, speeding up as it goes along, replicating the outward journey in reverse. Such an event is, from our experience just not going to happen, although energy would be conserved.
Another useful analogy is wealth. We are all aware that wealth is a measure of economic strength. Wealth is to the economic world as energy is to the natural world. Wealth can take many forms. It may be in the form of cars, jewels, property, money in the bank, or potential earnings. Nothing in the economic world can happen unless money is transferred (wealth is transferred). The currency of the UK economic world is the pound.
Similarly, energy can take many forms. It may be in the form of heat, or chemical potential energy, or even in the form of mass. Nothing in the natural universe can change unless energy is transferred. The currency of the natural world is the joule.
When an event, such as the purchase of a house takes place we never actually see the money transferred. We simply assume the transaction has taken place based on the effects we observe, namely the new owner takes up residence.
Similarly, when we observe a cup of coffee cooling down, we don't actually "see" joules of energy being transferred to the surrounding air, but we assume that this is happening based on the effects that we observe (the coffee getting cooler and the surrounding air getting warmer). In the natural world, the object at the higher energy potential (temperature in this case) can be considered to be in the driving seat.
The conclusion is that the conservation of energy law is insufficient to describe the constraints that apply to movement of heat energy. But there is another slightly more subtle law at work.
Temperature, pressure and the Gas Laws
In the early part of the nineteenth century engineers were thinking about the question of how much work could be obtained from a steam engine. It was commonly thought that a substance called caloric flowed from the hot side to the cold side in just the same way as water flows through a water wheel. By brilliant abstract thought the French physicist, Carnot, perceived that temperature provided the key.
He realised that the difference in temperature levels determines the amount of work that can be obtained from flow of heat. He proposed a Carnot Cycle, leading to the conclusion that the maximum possible efficiency of a heat engine depends only on its input and output temperature. Carnot developed the theory of heat engines in Réflexions sur la Puissance Motrice du Feu (Reflections on the Motive Power of Fire) in 1884.
Temperature and heat flow
Hotness and Coldness are familiar. A thermometer such as a mercury-in-glass type measures degrees of "hotness" by utilising the property of mercury which, like most things, expands when it gets hotter. As it expands, the column of mercury fills more of the tube, and so we can read off "how hot it is" on the scale. The scale is typically based on the melting point of ice and the boiling point of water. A Fahrenheit scale has the ice point marked 32 and the steam point marked 212 with 180 equal divisions or degrees. A Celsius or centigrade scale has the ice point at zero and the steam point at 100 degrees. The graduation of the glass tube can obviously be continued above and below these fixed points.
If the mercury rises 20 divisions above the 100 point on the Celsius thermometer, then the temperature is 120 degrees Celsius. But this extrapolation is limited in practice because if the temperature falls too low the mercury freezes. Different fluids can be used. Ethyl alcohol in glass can be used down to minus 166 degrees F while the electrical resistance of platinum wire can be used up to 1800 degrees.
We already noted that heat flows from a hot object (a brick) of its own accord to a cool one but never the other way. In order to make it do that we have to supply some additional high-grade energy and the question is how much? Imagine an experiment where a hot brick makes contact with a cool brick so that heat flows from one to the other. If we added the energy content of the hot brick and the cool brick at the end of the process, we would find that the cool brick, now slightly warmer, experienced less energy gain than the loss from the hot one, now slightly cooler. Some of the energy loss would be to surrounding atmosphere.
Where did that energy go? Due to inevitable imperfection of the heat exchange some energy would be uselessly frittered away to the atmosphere. These “losses” can be reduced by careful design of the experiment but never eliminated. We are going to ignore these losses because even without them the bricks can never reach exactly the same temperature.
Why? Heat movement requires a temperature difference (TD). This difference gets smaller and smaller as the losses are found and dealt with. So the “ideal” amount of heat transferred is known but never achieved. This ideal heat transfer is sometimes called “reversible” because the heat could just as easily flow in the opposite direction.
The next step is to note that on its journey from hot to cold, some of the energy can be transformed into work instead of just staying as heat at a lower temperature.
Efficiency in practice – the heat pump
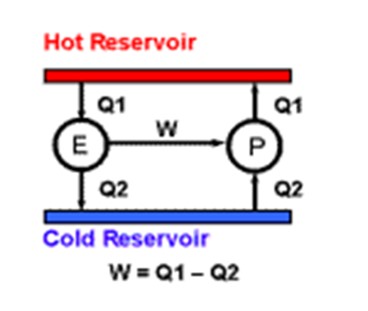The Minimum Amount of work to drive a heat pump is defined in terms of the Absolute Temperature Scale. A heat pump is any machine we may invent to transfer a given quantity of heat to a higher temperature, Imagine a hot reservoir and a cold reservoir. This heat pump P is taking a certain amount of energy in the form of work W that ends up as heat at the high temperature.
This is the best efficiency which can be obtained because if an engine E of greater efficiency producing more power could be devised, it could be used to drive the heat pump with extra work to spare.
This extra work would be, in effect, coming from nothing. We would have created a perpetual motion machine which is impossible. In this way Kelvin derived the value of absolute zero on our °C temperature scale to any number of decimal places, using calculus techniques.
In order to show this as simply as possible, consider a cycle working between two separate heat reservoirs, hot and cold, like the vapour compression cycle but keeping the process within the “dome” so that it is always in the saturated vapour/liquid phase and just touches the saturation curve. We want to apply the minimum amount of work to a piston in order to transfer heat from a cold reservoir so a hot reservoir. The cylinder contains the refrigerant.
The cycle is the complete process, we start at point 1. The piston is near the top of the cylinder and the fluid inside is 100% saturated vapour at high pressure and in contact with a hot reservoir H at the same temperature. Force the piston down, work is done on the system compressing the vapour and condensing it until all vapour is condensed. In a perfect or reversible process there is no temperature difference between the saturated vapour and the liquid.
The latent heat of condensation is transferred to the Hot reservoir, H, which is at the same temperature. At point 2 condensation is complete, When a system is undergoing change then the entropy change is equal to the heat absorbed by the system divided by the temperature at which change taken place
H is removed and the piston moves upwards, driven by expansion of the gas. The fluid pressure is allowed to fall to point 3 but no heat transfer takes place. The temperature falls due to the expansion of the fluid until it reaches exactly that of C, the cold body. This is point 3. When point 3 is reached, the cold body C is brought into contact with the cylinder and heat is transferred from the cold body to the fluid, which expands to point 4. Vapour is formed, pushing the piston upwards - the fluid is boiling at temperature C. Work is recovered. The cold body is removed at point 4 and the piston starts to move downward again, raising the pressure, but without heat transfer taking place, until point 1 is reached again.
The overall effect of the complete cycle is to transfer heat from the fluid from C at the lower temperature to the fluid at H, the higher temperature. Work is done on the piston because it has to be forced down against the higher pressure, but when it is moving upwards the pressure is lower. Less work is recovered. The net quantity of work is represented by the area of the diagram 1-2-3-4. This is a reversible cycle because at each stage heat transfer occurs between the reservoirs and the fluid when both are the same temperature. It defines limiting case. In practice a measurable quantity of heat will only flow if there is a temperature difference.
Kelvin was considering the maximum work that could be obtained from the clockwise reversible cycle i.e. a heat engine rather than a heat pump. Kelvin had to evaluate the ratio of the work output to the heat absorbed during the cycle consisting entirely of reversible processes. The possibility that the Carnot function could be the temperature as measured from a zero temperature, was suggested by Joule in a letter to Kelvin. This allowed Kelvin to establish his absolute temperature scale. Using temperature values on this scale he was able to confirm that the efficiency of the cycle depended only on the two temperatures:
Efficiency = work done/total heat supplied, (Th-Tc)/Th.
The work produced by the system is the difference between the heat absorbed from the hot reservoir and the heat given up to the cold reservoir. Even in this ideal cycle some energy must be supplied to make the heat flow from the cold to the hot reservoir.
Getting work from heat flow
The driving “force” behind heat movement is a function of the difference in temperature of the two bodies.
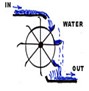Let’s take an analogy. Water flowing from high level to low level can do useful work. It can turn a wheel that is connected to a weight lifter for example. The larger the difference in water levels, the larger the amount of work. It’s easy to see that this release of potential energy (high level water to low level) is converted into work by a water-wheel. But the water has to flow away from the wheel at the bottom. So. some of the potential energy must be converted to the water’s kinetic energy. That amount doesn’t help to lift the weight. Before moving on and considering the Carnot cycle and its relevance to refrigeration, we need to be clear about the behaviour of liquids, gases and the change of state from liquid to gas.
Pressure
Water boils at a temperature of 100°C. We say that it changes phase from a liquid to a gas. The heat has to be at 100°C or more to boil water, but other substances boil at lower temperatures. This will come in handy as we shall see when we take a look at the effect of pressure on boiling point.
Condensation is the reverse of boiling. The steam gives up its heat and turns back to water. When we mix steam with air, which is what happens when the kettle boils, the cool air tends to condense the steam, and very small droplets of water form. This is what we see and commonly call 'steam'. Pure steam is a colourless gas.
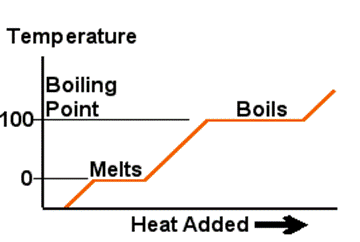Many substances follow the process shown in the diagram when starting from a solid state and adding heat continuously at a constant rate. At the boiling point and freezing point heat energy is used to change the state until this process is complete and then the temperature starts to rise once more. When heat is being added to raise the temperature, it's called Sensible Heat. When the heat is being added to melt ice or boil the water it's called Latent Heat. Sensible?
These are not theories. They are descriptions of what we observe. You can observe them!
We’ll focus on the boiling process because most refrigeration applications make use of boiling refrigerant to absorb heat. Each substance has its own boiling point: water is 100°C, alcohol is about 80°C.
An increase in pressure raises the boiling point. Water in a kettle on a mountain top it boils at a lower temperature because the atmospheric pressure is lower. In a steam boiler the pressure is maintained well above atmospheric, so the steam starts out at a very high temperature.
Enthalpy
Enthalpy is the term used to describe the amount of energy a substance holds. Like temperature the scale it is arbitrary, but based on a defined value at a certain pressure and temperature. Normally enthalpy difference is all that is required. Enthalpy measured in Joules per unit mass.
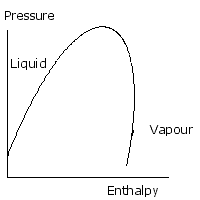The key to understanding a typical refrigeration process is mastery of this diagram. Detailed property values may be found from tables and digital sources but without an understanding of where they apply their value is limited. This diagram is a way of describing the liquid and gas phase of a substance. On the vertical axis is pressure, and on the horizontal, enthalpy. Enthalpy can be thought of as the quantity of heat in a given quantity, or mass of substance. The curved line is called the saturation curve and it defines the boundary of pure liquid and pure gas, or vapour. The region marked vapour the substance exists as a vapour or gas. In the region marked liquid, it’s a liquid. If the pressure rises so that we are considering a region above the top of the curve, there is no distinction between liquid and vapour. Above this point pressure the gas cannot be liquefied. This is called the Critical Pressure. In the region underneath the curve, there is a mixture of liquid and vapour. In order to understand how this diagram is used, let’s consider water turning into steam in the kettle.
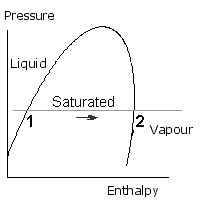The boiling of water, or vaporization of refrigerant is a constant pressure process, and is represented by a horizontal line as shown. The water (or liquid refrigerant) starts off on the left side and as it warms up it approaches the left hand side of the saturation curve. At point 1 it starts to boil (like the kettle). Heat continues to be added so the condition point is still moving along towards the right. When point 2 is reached, all the liquid has turned into vapour. Point 2 is saturated vapour, because it only just contains sufficient enthalpy to be 100% vapour. If more heat is added, the vapour becomes hotter, this is called Superheated Vapour.
Condensation occurs when the vapour turns back to liquid. The vapour starts off on the right hand side and as it cools down it approaches the right hand side of the saturation curve. At point 3 it starts to condense and this continues until point 4 when all the vapour has turned into liquid. Point 4 is saturated liquid. If more heat is removed, the liquid cools. It is then called subcooled liquid.
Condensation is shown at a higher pressure than evaporation, but either process may take place at any pressure below the critical pressure.
The Vapour Compression Cycle
Evaporation and condensing are useful processes because they allow relatively large quantities of heat to be transferred in and out of constant temperature “reservoirs”. The liquid refrigerant evaporates at low pressure (1 -2) providing cooling as it evaporates at a lower temperature than that of the cold space. The resulting vapour is compressed to the higher pressure (2-3). This raises its temperature, usually well into the superheat region as shown. This heat then flows to the atmosphere causing its temperature reduction and condensation (3-4). At the higher pressure the refrigerant becomes high pressure liquid (4). To complete the cycle the high pressure liquid is simply passed through an expansion control valve back to the evaporator (4-1). Most of it is still liquid but some vapour is formed. The relative quantities are defined by the shape and position of the curved line for the particular substance.
The Second Law of Thermodynamics
Carnot was not completely right because heat cannot be thought of as a substance which is conserved. The same amount of water flows away from a water wheel as enters it. But we now know that less heat flows away from an engine than is put into water by the furnace.
Joule showed what had happened to this lost heat. It had turned into work! This discovery, and the subsequent pioneering investigations by Clausius in Germany and Thompson (later Lord Kelvin) in Scotland resulted in the Second Law of Thermodynamics, which tells us the maximum proportion of the heat it is possible to turn into work.
It was realised that there must be a lowest theoretically possible temperature, absolute zero. It may be thought of as the temperature at which the brick contains heat energy. The molecules which ‘bounce around’ in a substance have finally come to rest.
Entropy
Now we are in better position to talk about entropy - a more difficult concept. We showed that there were always some ‘losses’ when our hot gold brick was allowed to transfer heat energy to a cooler one. These so-called losses do not constitute a loss of energy because energy cannot be created or destroyed (first law of physics). If it could, the brick would end up at absolute zero, whereas we know from experience that its temperature will only fall as far as that of its surrounds, assuming they are big enough to absorb the transferred energy with negligible rise in temperature.” Negligible” is the key word here. We know that the brick will end up at room temperature but however closely we examine the temperature difference we find it becomes vanishingly small but never quite makes it to zero. Nevertheless we know the brick’s final temperature – very close to room temperature – to whatever accuracy we want. The ‘ideal’ heat exchange process takes place when the TD (temperature differential) is vanishingly small.
This is termed a reversible heat transfer process because the heat could be flowing in the opposite direction if there were no TD.
We noted that energy can take various forms. So as well as the amount of energy stored in an object, its usefulness depends on its degradation potential. Heat energy is low-grade. There is nowhere for it to go but heat at a lower temperature. Although all forms of energy are interconvertible, and all can be used to do work, it is not always possible, even in principle, to convert the entire available energy into work. Entropy is a measure of how much energy is not available to do work.
Steam engine analogy
Remember the scientists of this period were looking for more power from steam engines. Refrigeration was at an early stage with Air, Water, then CO2 or ammonia. Pressure can be thought of as the average speed with which the molecules in a substance are moving. They are moving in random directions and in any perceptible size of system there are millions and millions of them. Work is more ordered. The piston moves against the restraining force of accelerating a locomotive for example. To make that piston move we have to slow down, statistically, a whole bunch of gas molecules, many more than in the piston, because they are randomly distributed in the gas. As soon as the piston moves the volume of the cylinder increases and the gas molecules are left with a lower average velocity – in other words the gas has cooled down.
The entropy of an ideal gas is proportional to the number of gas molecules N. The number of molecules in twenty liters of gas at room temperature and atmospheric pressure is roughly N ≈ 6×1023 (the Avogadro number).
The second law of thermodynamics states that the entropy of an isolated system never decreases.
Understanding why requires introducing a concept called entropy. By examining it, we shall see that the directions associated with the second law—heat transfer from hot to cold, for example—are related to the tendency in nature for systems to become disordered and for less energy to be available for use as work.
Bouncing ball analogy
Another everyday example using potential energy conversion: let go of a bouncy ball at height from a hard floor. It bounces back upwards. But does it return to its starting point? No, we never experience that. We can get closer and closer by reducing friction, making the ball more bouncy, or the floor harder. This does not prevent the evaluation of the limiting condition or reversible process when the ball returns to its starting point. When the object is dropped, some of that potential energy gets converted into movement of air molecules as the object passes through them. At the start, entropy is low and all the energy is stored in the form of potential energy in the object. The total amount of energy has not changed but the it is now more spread out. The energy is less usable and entropy has increased.
Closed systems
The second law tells us that transfer of energy from a high level to a lower one results in an increase of entropy, higher temperature heat is more valuable than lower temperature heat.
In yet another example, start with a quantity m of gas in a closed container, A, at pressure P. The molecules are bouncing around and hitting the wall with a certain average velocity. The gas has a certain amount of stored energy. We use the term ‘closed’ in the strict sense of meaning that it is totally isolated from the outside world. The gas is equally spread out inside. If the volume of the container is reduced increased the pressure increases. To maintain the pressure more gas is needed.